
In this section, we’ll use data from a tensile test to build a stress strain curve with Python and Matplotlib.
A tensile test is a type of mechanical test performed by engineers used to determine the mechanical properties of a material. Engineering metal alloys such as steel and aluminum alloys are tensile tested in order to determine their strength and stiffness. Tensile tests are performed in a piece of equipment called a mechanical test frame.

After a tensile test is complete, a set of data is produced by the mechanical test frame. Using the data acquired during a tensile test, a stress-strain curve can be produced.
In this post, we will create a stress-strain curve (a plot) from a set of tensile test data of a steel 1045 sample and an aluminum 6061 sample. The stress strain curve we construct will have the following features:
We will construct our stress strain curve using a Jupyter notebook.
Make sure to save your Jupyter notebook with a recognizable name.
Next, we need to download the two data files that we will use to build our stress-strain curve. You can download sample data using the links below:
After these .xls files are downloaded, both .xls files need to be moved into the same folder as your running Jupyter notebook.
Now that a Jupyter notebook is open and the two .xls data files are in the same folder as the Jupyter notebook, we can start coding and build our plot.
At the top of the Jupyter notebook, import NumPy, Pandas and Matplotlib. The command %matplotlib inline is included so that our plot will display directly inside our Jupyter notebook. If you are using a .py file instead of a Jupyter notebook, make sure to comment out %matplotlib inline as this line is not valid Python code.
# imports import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy.stats import linregress %matplotlib inline
Before we proceed, it’s a good idea make sure the two .xls data files are in the same folder as our running Jupyter notebook.
We’ll use a Jupyter notebook magic command to print out the contents of the folder that our notebook is in. The %ls command lists the contents of the current folder.
ABS_HIPS_plot_with_error_bars.png Al60601_raw_data.xls Steel1018_raw_data.xls bar_plot_with_error_bars.ipynb calculate-yield-strength-programmatically.ipynb images/ mechanical-properties-from-stress-strain-curves.ipynb mechanical-properties-intro.md plotting-stress-strain-curves.ipynb stress-strain_curve.png stress_strain_curve_with_inset.png stress_strain_curve_with_inset_elastic_region.ipynb
We can see the two .xls data files Al60601_raw_data.xls and Steel1018_raw_data.xls are in our current folder.
Now that we are sure the two .xls data files are in the same folder as our notebook, we can import the data in the two two .xls files using Panda’s pd.read_excel() function. The data from the two excel files will be stored in two Pandas dataframes called steel_df and al_df . A Panda’s dataframe is a tabular data type.
We can use Panda’s .head() method to view the first five rows of each dataframe.
df_al = pd.read_excel('Al60601_raw_data.xls') df_al.head()
WARNING *** OLE2 inconsistency: SSCS size is 0 but SSAT size is non-zero
| TESTNUM | POINTNUM | TIME | POSIT | FORCE | EXT | CH5 | CH6 | CH7 | CH8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 542 | 1 | 8.470 | 0.02256 | 201.146011 | -0.001444 | 0.007552 | NaN | NaN | NaN |
| 1 | 542 | 2 | 8.632 | 0.02330 | 206.599442 | 0.000302 | 0.007552 | NaN | NaN | NaN |
| 2 | 542 | 3 | 10.027 | 0.02846 | 287.512573 | 0.003044 | 0.018898 | NaN | NaN | NaN |
| 3 | 542 | 4 | 11.031 | 0.03232 | 365.380981 | 0.009881 | 0.022061 | NaN | NaN | NaN |
| 4 | 542 | 5 | 11.928 | 0.03616 | 447.813965 | 0.014085 | 0.033652 | NaN | NaN | NaN |
df_steel = pd.read_excel('Steel1018_raw_data.xls') df_steel.head()
WARNING *** OLE2 inconsistency: SSCS size is 0 but SSAT size is non-zero
| TESTNUM | POINTNUM | TIME | POSIT | FORCE | EXT | CH5 | CH6 | CH7 | CH8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 523 | 1 | 6.189 | 0.07302 | 202.924728 | 0.000402 | -0.028272 | NaN | NaN | NaN |
| 1 | 523 | 2 | 6.549 | 0.07396 | 205.714890 | -0.000238 | -0.034549 | NaN | NaN | NaN |
| 2 | 523 | 3 | 7.148 | 0.07624 | 217.763336 | -0.000713 | -0.030140 | NaN | NaN | NaN |
| 3 | 523 | 4 | 9.146 | 0.08438 | 316.306122 | 0.002377 | -0.025968 | NaN | NaN | NaN |
| 4 | 523 | 5 | 10.041 | 0.08822 | 417.003357 | 0.003089 | -0.024100 | NaN | NaN | NaN |
We see a number of columns in each dataframe. The columns we are interested in are FORCE, EXT, and CH5. Below is a description of what these columns mean.
Next we’ll create a four Pandas series from the CH5 and FORCE columns of our df_al and df_steel dataframes.
The equations below show how to calculate stress, σ, and strain, ϵ, from force F and cross-sectional area A. Cross-sectional area A is the formula for the area of a circle. For the steel and aluminum samples we tested, the diameter d was 0.506 in.
\[ \sigma = \fracRemember that exponents in Python use a double asterix ** .
d = 0.506 r = d/2 A = np.pi*r**2 stress_al = (df_al['FORCE']/A)*0.001 strain_al = df_al['CH5']*0.01 stress_steel = (df_steel['FORCE']/A)*0.001 strain_steel = df_steel['CH5']*0.01
Now that we have the data from the tensile test in four series, we can build a quick plot using Matplotlib’s ax.plot() method. The first x,y pair we pass to ax.plot() is strain_al , stress_al and the second x,y pair we pass in is strain_steel , stress_steel . The command plt.show() shows the plot.
fig,ax = plt.subplots() ax.plot(strain_al, stress_al, strain_steel, stress_steel) plt.show()
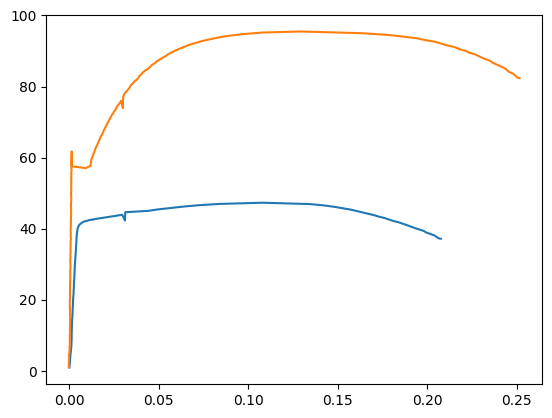
We see a plot with two lines. One line represents aluminum 6061 and one line represents steel 1018. We can improve our plot by adding axis labels with units, a title and a legend.
Axis labels, titles and a legend are added to our plot with three Matplotlib methods. The methods are summarized in the table below.